Featured
The compelling mathematical challenge of the three-body problem
By Tim Stephen
UC Santa Cruz
August 8, 2019 — Santa Cruz, CA
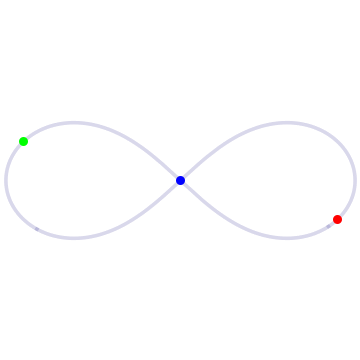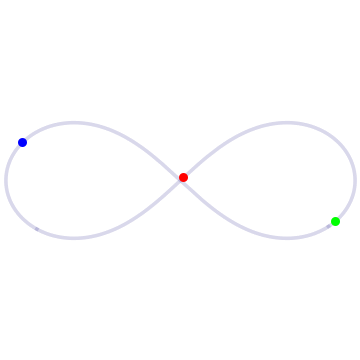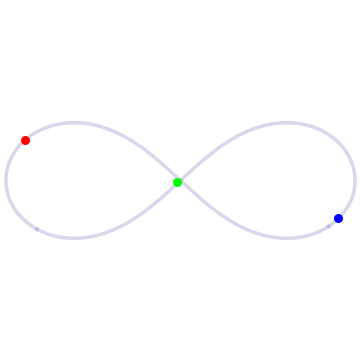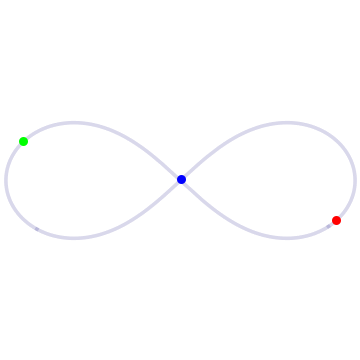
(Photo above: In the figure-eight solution to the three-body problem, three bodies of equal mass chase each around a figure-eight loop. Source: UCSC website)
For mathematician Richard Montgomery, falling cats and orbiting planets have led to fruitful lines of research
From its origins more than 300 years ago in Newton’s work on planetary orbits, the three-body problem has blossomed into a rich subject that continues to yield new insights for mathematicians.

Richard Montgomery, professor of mathematics at UC Santa Cruz, calls the “three-body problem” one of the classic quandaries in mathematical history. (Source: UCSC website)
Richard Montgomery, a distinguished professor of mathematics at UC Santa Cruz, calls it one of the classic quandaries in mathematical history. In an article in the August issue of Scientific American, he recounts the history of the three-body problem and the progress that he and other mathematicians have made in the past two decades.
“It has challenged people for centuries, and that’s partly what makes it interesting. You’re adding to the work of people like Newton and Poincaré and Lagrange,” Montgomery said.
The fundamental problem is to predict the motions of three bodies (such as stars or planets) mutually attracted by gravity, given their initial positions and velocities. It turns out that a general solution to the problem is essentially impossible due to chaotic dynamics, which Henri Poincaré discovered in 1890.
“There are solutions for special cases, but there’s not a simple formula to give you a general solution,” Montgomery explained.
From the practical standpoint of predicting planetary orbits and planning space missions, approximations can be calculated with a high degree of accuracy using computers and a process called numerical integration. That may be good enough for NASA, but not for mathematicians, whose continued explorations of the problem have led to important advances in mathematics.
Falling cats
The three-body problem ties together three different branches of mathematics: topology, geometry, and dynamics. Montgomery said that was what got him interested in it more than 20 years ago. He had been working on questions related to the mathematics and physics of how a cat lands on its feet, which has applications in control theory and satellite orientation.
“I kept simplifying the problem until the cat consisted of just three point masses,” Montgomery said. Then a colleague referred him to another mathematician who had been working on similar ideas, and before long he had switched from falling cats to celestial mechanics. Hearing that the best people working on celestial mechanics were in Paris, Montgomery spent a sabbatical there working with Alain Chenciner at Paris Diderot University on the three-body problem.
One of their first major results, published in 2000, was a rediscovery and proof of a figure-eight-shaped solution, in which three bodies of equal mass chase one another endlessly around a figure-eight loop. Although Chris Moore of the Santa Fe Institute had first found this solution in 1993, using a numerical approximation method, its rediscovery by Montgomery and Chenciner had a much bigger impact on the field.
“We were able to give a rigorous existence proof of the figure-eight solution, and the way we did it allowed others to generalize the solution and find a lot of other interesting things,” Montgomery explained.
A more general statement of the three-body problem for any number of bodies greater than two is called the N-body problem. Montgomery said when he first presented the three-body figure-eight solution at a conference, a member of the audience quickly pointed out how it should work for four bodies. Soon, mathematicians were discovering a diverse array of new orbits for the equal-mass N-body problem. These periodic solutions in which all of the masses chase each other around a fixed, closed curve without collisions were named “choreographies” by Spanish mathematician Carles Simó, who has discovered hundreds of them.
“It created a mini-industry, so that we now know vast numbers of these choreographies,” Montgomery said.
New direction
Years later, Simó helped send Montgomery’s research on the three-body problem in a new direction by suggesting he look for dynamical mechanisms underlying the periodic solutions. This led to a productive collaboration in recent years with Rick Moeckel of the University of Minnesota.
The new mathematical ideas that have emerged from Montgomery’s work on the three-body problem do not have practical applications, at least not yet. It is often the case that abstract mathematical concepts are developed long before anyone finds a practical use for them.
Many people have been captivated by the aesthetic appeal of the figure-eight solution and other choreographies. The concept has even made its way into science fiction through Chinese author Liu Cixin, whose novel The Three-Body Problem won the Hugo Award in 2015.
But Montgomery says he would never have tackled the problem if he had not had tenure.
“It’s such a hard problem, and you don’t know if you’re going to make any progress,” he said. “But persistence pays off sometimes. So I appreciate the tenure system, and also being able to take sabbaticals to work with collaborators. There’s something about physically meeting people that is so important for working together.”
In his Scientific American article, Montgomery provides not only a detailed description of the three-body problem, but also a fascinating story of the international collaborations and personal relationships that enabled him to make progress on this compelling mathematical conundrum.
###
Tagged UC Santa Cruz








